Schultz Dale Reaction

July 26, 2020October 21, 2013 by Anand Bhumkar

Click on the image to know more about Schultz Dale Reaction

What is Schultz Dale Reaction

Schultz Dale reaction is an anaphylactic reaction produced in vitro during the testing of immunomodulatory drugs

What is the rationale behind Schultz Dale Reaction

It is used to initiate the release of mediators of anaphylaxis like histamine which induce contraction in smooth muscles.

How is Schultz Dale Reaction induced

To induce Schultz Dale reaction, guinea pigs are used generally. The animals are sensitized against egg albumin and three weeks after this, they are sacrificed. Ileum of the sacrificed animals is isolated and the contractility of the isolates is tested

Can we use any other tissues for Schultz Dale reaction?
Yes. Researchers have used lungs, tracheae of guinea pigs and trachea of mice as well.

|Humidity|- Absolute, Relative and Specific.

July 26, 2020April 18, 2012 by Anand Bhumkar

Humidity

Humidity is a term for water vapor in the air, and can refer to any one of several measurements of humidity.

Absolute humidity

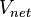Absolute humidity is an amount of water vapor, usually discussed per unit volume. The mass of water vapor, $m_w$ , per unit volume of total moist air, $V_{net}$ , can be expressed as follows:

$AH = {m_w \over V_{net}}.$

Absolute humidity in air ranges from zero to roughly 30 grams per cubic meter when the air is saturated at 30 °C.

Relative humidity

Relative humidity is a term used to describe the amount of water vapor in a mixture of air and water vapor. It is defined as the ratio of the partial pressure of water vapor in the air-water mixture to the saturated vapor pressure of a flat sheet of pure water at those conditions. The relative humidity of air depends not only on temperature but also on the pressure of the system of interest.

Relative humidity is normally expressed as a percentage and is calculated by using the following equation, it is defined as the ratio of thepartial pressure of water vapor (H₂O) $\left({e_w}\right)$ in the mixture to the saturated vapor pressure of water $\left({{e^*}_w}\right)$ at a prescribed temperature.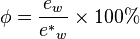

$\phi = {{e_w} \over {{e^*}_w}} \times 100%$

Relative humidity is often used instead of absolute humidity in situations where the rate of water evaporation is important, as it takes into account the variation in saturated vapor pressure.

Specific humidity

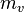Specific humidity is the ratio of water vapor to dry air in a particular mass, and is sometimes referred to as humidity ratio. Specific humidity ratio is expressed as a ratio of mass of water vapor, $m_v$ , per unit mass of dry air $m_a$ .

That ratio is defined as:

$SH = {m_v \over m_a}.$

Dissolution

July 26, 2020April 18, 2012 by Anand Bhumkar

Dissolution

Dissolution is the process by which a solid, liquid or gas forms a solution in a solvent. For the dissolution of solids, the process of dissolution can be explained as the breakdown of the crystal lattice into individual ions, atoms or molecules and their transport into the solvent

The rate of dissolution quantifies the speed of the dissolution process.

The rate of dissolution depends on:

nature of the solvent and solute
temperature (and to a small degree pressure)
degree of undersaturation
presence of mixing
interfacial surface area
presence of inhibitors (e.g., a substance adsorbed on the surface).

The rate of dissolution can be often expressed by the Noyes-Whitney Equation or the Nernst and Brunner equation^[1] of the form:

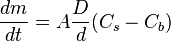
$\frac {dm} {dt} = A \frac {D} {d} (C_s-C_b)$

where:

m – amount of dissolved material, kg

t – time, seconds

A – surface area of the interface between the dissolving substance and the solvent, m²

D – diffusion coefficient, m²/s

d – thickness of the boundary layer of the solvent at the surface of the dissolving substance, m

C_s – concentration of the substance on the surface, kg/m³

C_b – concentration of the substance in the bulk of the solvent, kg/m³

For dissolution limited by diffusion, C_s is equal to the solubility of the substance.

When the dissolution rate of a pure substance is normalized to the surface area of the solid (which usually changes with time during the dissolution process), then it is expressed in kg/m²s and referred to as “intrinsic dissolution rate”. The intrinsic dissolution rate is defined by the United States Pharmacopeia.

Dissolution rates vary by orders of magnitude between different systems. Typically, very low dissolution rates parallel low solubilities, and substances with high solubilities exhibit high dissolution rates, as suggested by the Noyes-Whitney equation. However, this is not a rule.

Diffusion

July 26, 2020April 18, 2012 by Anand Bhumkar

Diffusion describes the spread of particles through random motion from regions of higherconcentration to regions of lower concentration. The time dependence of the statistical distribution in space is given by the diffusion equation. The concept of diffusion is tied to that of mass transferdriven by a concentration gradient. Diffusion is invoked in the social sciences to describe the spread of ideas.

Fick’s laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.

Fick’s first law relates the diffusive flux to the concentration under the assumption of steady state. It postulates that the flux goes from regions of high concentration to regions of low concentration, with a magnitude that is proportional to the concentration gradient (spatial derivative). In one (spatial) dimension, the law is

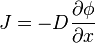
$\bigg. J = - D \frac{\partial \phi}{\partial x} \bigg.$

where

$J$ is the “diffusion flux” [(amount of substance) per unit area per unit time], example $(\tfrac{\mathrm{mol}}{ \mathrm m^2\cdot \mathrm s})$ . $J$ measures the amount of substance that will flow through a small area during a small time interval.

$\, D$ is the diffusion coefficient or diffusivity in dimensions of [length² time⁻¹], example $(\tfrac{\mathrm m^2}{\mathrm s})$

$\, \phi$ (for ideal mixtures) is the concentration in dimensions of [(amount of substance) length⁻³], example $(\tfrac\mathrm{mol}{\mathrm m^3})$

$\, x$ is the position [length], example $\,\mathrm m$

Fick’s second law predicts how diffusion causes the concentration to change with time:

$\frac{\partial \phi}{\partial t} = D\,\frac{\partial^2 \phi}{\partial x^2}\,\!$

Where

$\,\phi$ is the concentration in dimensions of [(amount of substance) length⁻³], example $(\tfrac\mathrm{mol}{m^3})$
$\, t$ is time [s]
$\, D$ is the diffusion coefficient in dimensions of [length² time⁻¹], example $(\tfrac{m^2}{s})$
$\, x$ is the position [length], example $\,m$

Supersaturation

July 26, 2020April 17, 2012 by Anand Bhumkar

The term “supersaturatio” refers to a solution that contains more of the dissolved material than could be dissolved by the solvent under the solubility amount. It can also refer to a vapor of a compound that has a higher (partial) pressure than the vapor pressure of that compound.

Solubility

July 26, 2020April 17, 2012 by Anand Bhumkar

Solubility

Solubility is the property of a solid, liquid, or gaseous chemical substance called solute to dissolve in a solid, liquid, or gaseous solvent to form a homogeneous solution of the solute in the solvent.

Ames Test

July 26, 2020April 10, 2012 by Anand Bhumkar

The Ames test measures the reversion from mutant to wild type form (back-mutation) in a culture of Salmonella. The test is used to screen large numbers of compounds for their potential mutagenicity.

What is Schultz Dale Reaction

What is the rationale behind Schultz Dale Reaction

How is Schultz Dale Reaction induced

Humidity

Absolute humidity

Relative humidity

Specific humidity

Dissolution

Dissolution is the process by which a solid, liquid or gas forms a solution in a solvent. For the dissolution of solids, the process of dissolution can be explained as the breakdown of the crystal lattice into individual ions, atoms or molecules and their transport into the solvent

The rate of dissolution quantifies the speed of the dissolution process.

The rate of dissolution depends on:

nature of the solvent and solute

temperature (and to a small degree pressure)

degree of undersaturation

presence of mixing

interfacial surface area

presence of inhibitors (e.g., a substance adsorbed on the surface).

The rate of dissolution can be often expressed by the Noyes-Whitney Equation or the Nernst and Brunner equation[1] of the form:

where:

m – amount of dissolved material, kg

t – time, seconds

A – surface area of the interface between the dissolving substance and the solvent, m2

D – diffusion coefficient, m2/s

d – thickness of the boundary layer of the solvent at the surface of the dissolving substance, m

Cs – concentration of the substance on the surface, kg/m3

Cb – concentration of the substance in the bulk of the solvent, kg/m3

For dissolution limited by diffusion, Cs is equal to the solubility of the substance.

Dissolution rates vary by orders of magnitude between different systems. Typically, very low dissolution rates parallel low solubilities, and substances with high solubilities exhibit high dissolution rates, as suggested by the Noyes-Whitney equation. However, this is not a rule.

Fick’s laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.

where

is the “diffusion flux” [(amount of substance) per unit area per unit time], example . measures the amount of substance that will flow through a small area during a small time interval.

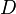is the diffusion coefficient or diffusivity in dimensions of [length2 time−1], example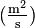

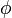(for ideal mixtures) is the concentration in dimensions of [(amount of substance) length−3], example

is the position [length], example

Fick’s second law predicts how diffusion causes the concentration to change with time:

Where

is the concentration in dimensions of [(amount of substance) length−3], example

is time [s]

is the diffusion coefficient in dimensions of [length2 time−1], example

is the position [length], example

Solubility

The rate of dissolution can be often expressed by the Noyes-Whitney Equation or the Nernst and Brunner equation^[1] of the form:

A – surface area of the interface between the dissolving substance and the solvent, m²

D – diffusion coefficient, m²/s

C_s – concentration of the substance on the surface, kg/m³

C_b – concentration of the substance in the bulk of the solvent, kg/m³

For dissolution limited by diffusion, C_s is equal to the solubility of the substance.

$J$ is the “diffusion flux” [(amount of substance) per unit area per unit time], example $(\tfrac{\mathrm{mol}}{ \mathrm m^2\cdot \mathrm s})$ . $J$ measures the amount of substance that will flow through a small area during a small time interval.

$\, D$ is the diffusion coefficient or diffusivity in dimensions of [length² time⁻¹], example $(\tfrac{\mathrm m^2}{\mathrm s})$

$\, \phi$ (for ideal mixtures) is the concentration in dimensions of [(amount of substance) length⁻³], example $(\tfrac\mathrm{mol}{\mathrm m^3})$

$\, x$ is the position [length], example $\,\mathrm m$

$\,\phi$ is the concentration in dimensions of [(amount of substance) length⁻³], example $(\tfrac\mathrm{mol}{m^3})$

$\, t$ is time [s]

$\, D$ is the diffusion coefficient in dimensions of [length² time⁻¹], example $(\tfrac{m^2}{s})$

$\, x$ is the position [length], example $\,m$